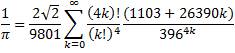Así pueden empezar las cosas

En esta viñeta, la protagonista es la Ciencia en general.

    

Último récord sobre Pi

Por casualidad he descubierto este artículo:

http://www.cadenaser.com/cultura/articulo/record-computacion-cifras-numero-pi/csrcsrpor/20110121csrcsrcul_4/Tes

según el cual, se han calculado, nada más y nada menos, que  5 billones de decimales del número pi con un ordenador personal, lo que llevó 90 días el verano pasado. Buscando un poco más, resulta que se tratan de dos personas: Alexader J. Yee (americano) y Shigeru Kondo (japonés).
Ninguno de los dos es matemático: Yee es un estudiante de de 23 años de Informática y Kondo, de 55, es ingeniero informático.  ¿Por qué decidieron embarcarse en esa tarea? Según ellos mismos: "Porque es pi... Y porque pueden hacerlo" Dicho de otro modo, para poner a prueba hasta dónde pueden llegar . Pero aún no han llegado al límite, sino que tiene proyectado llegar a los 10 billones de decimales.

Una curiosidad: según he leido, trabajaron juntos en el proyecto a través de correo electrónico.

Aunque la página es en inglés, aquí se pueden ver detalles tanto el hardware y el software, como del método matemático utilizado: http://www.numberworld.org/misc_runs/pi-5t/details.html#purpose

De dicha página he cogido este pequeño estracto:

3.

1415926535 8979323846 2643383279 5028841971 6939937510 : 50 5820974944 5923078164 0628620899 8628034825 3421170679 : 100

2962457053 9070959679 6673211870 6342459769 2128529850 : 999,999,999,950 2976735807 0882130902 2460461146 5810642210 6680122702 : 1,000,000,000,000

9354516713 6069123212 1286195062 3408400370 1793492657 : 1,999,999,999,950 8386341797 9368318191 5708299469 1313121384 3887908330 : 2,000,000,000,000

3840840269 5893047555 2627475826 8598006396 3215856883 : 2,699,999,989,950 9256371619 3901058063 3448436720 6294374587 7597230153 : 2,699,999,990,000 8012497961 5892988915 6174704230 3863302264 3931687863 : 2,699,999,990,050 3126006397 8582637253 6739664083 9716870851 0983536511 : 2,699,999,990,100

5628334110 5221005309 8638608325 4364661745 5833914321 : 2,999,999,999,950 9150024270 6285788691 0228572752 8179710957 7137931530 : 3,000,000,000,000

5209957313 0955102183 1080456596 1489168093 0578494464 : 3,999,999,999,950 3638467628 3610607856 5071920145 5255995193 8577295739 : 4,000,000,000,000

2597691971 6538537682 7963082950 0909387733 3987211875 : 4,999,999,999,950 6399906735 0873400641 7497120374 4023826421 9484283852 : 5,000,000,000,000

Según los autores, las fórmulas utilizadas en el programa para calcular pi fueron:

• Fórmula de Chudnovsky

• Fórmula de Ramanujan:

Sin quitarle mérito a lo que han hecho, siguen quedando infinitas cifras por hallar...Y aunque no signifique mucho... Ya sabemos que la 5000000000000 cifra decimal es un 2.

Y como "hay gente pa to", dejo colgado este video donde a una chica de 16 años recita las 2000 cifras decimales de pi... Lo mejor de todo es que lo hace para un concurso de Matemáticas. Por supuesto, esta es sólo la primera parte... Las otras dos las dejo a la imaginación y en todo caso se pueden buscar en el google.

También hay otro video donde otra niña recita las 500 primeras cifras decimales en 90 s... Ante esto, la verdad, prefiero el de fotografía matemática...

Lo que es sumergirse en un examen...

La derivada es un concepto que no enseño este año en clase, pero no me resisto a colgar este vídeo, que es un puntazo. De todas formas, en 4º he mencionado "derivada" después de hablar de la T.V.M., así que, ya tengo una excusa.

¿Para qué conocer los números primos?

A raíz de la entrevista que hicieron en Redes a Marcus du Sautoy, busqué más información sobre este y he descubierto también el video que dejo colgado. En su momento lo comenté en alguna clase y le comenté a uno de mis alumnos (Alejandro Gavira) que ya lo pondría en el blog. Merece la pena, aunque sea, echar un vistazo. Desde 1º de ESO nos dicen lo que es un número primo y nos dan la lata con que tenemos que aprender a poner los demás números en función de ellos (lo que se llama factorizar números). Por ejemplo: 15=3·5, 9=3^2... Hay quienes se resisten por todos los medios y pasan del tema... Y hay quien acaba aprendiendo a factorizar números porque, después de todo, tampoco requiere un esfuerzo mental alucinante... Por supuesto, en el caso de los números que trabajamos en ESO, que son bastante pequeños. Sabiendo factorizar, seguimos recurriendo a los números primos para calcular m.c.m. y sumar fracciones... Después, pasamos un tupido velo sobre ellos y pasamos a tratar otros conceptos matemáticos, nos "olvidamos" de ellos. Pero... ¿eso es todo lo que hay sobre números primos?

Marcus du Sautoy nos revela que no... "Solo eso, no" hay mucho más. Para empezar, los números primos constituyen aún hoy en día uno de los problemas matemáticos más importantes. Aunque pueda sonar extraño, hoy en día existen matemáticos que se dedican a resolver tal problema: descubrir el patrón que siguen los números primos o, dicho de otra forma, descubrir una "fórmula" con la que obtenerlos todos (hay infinitos) Pero aún hay más, los números primos están mucho más presentes en nuestra sociedad de lo que en un principio podamos imaginar. Esto, más y mejor contado es lo que hace Marcus du Sautoy en el siguiente video. Así es, una de los temas más fáciles de la ESO es la base de uno de los problemas más difíciles e importantes de la historia y de la actualidad.

Du Sautoy es un matemático de la Universidad de Oxford y que se dedica al problema de los números primos. Además también se dedica a la divulgación de las Matemáticas, escribiendo libros y apareciendo en documentales ("La historia del 1") y en televisión, lo cual es de agradecer. También he descubierto una página suya dedicada a los números primos. Está en inglés, pero creo que este es fácil. Dejo el enlace:

http://www.musicoftheprimes.com/

Dentro del enlace, clicad sobre "Prime importance" y en el menú de la derecha aparece "Prime games". Recomiendo el "Shooting primes" y "Prime number mazes"

Desgraciadamente, no he podido bajarme el video entero, pero tiempo al tiempo... Además, los otros 3 capítulos pueden verse, por ejemplo, en  "youtube"
Sin erollarme más, aquí está el video:

La música de los números primos. Capítulo 1 from ramicao on Vimeo.

El punto azul pálido

Revisando una antigua entrada del blog, se me ocurrió ligarla con este vídeo. Es muy cortito y tiene ya sus años, pero no por eso deja de ser muy recomendable. La voz de fondo es de Carl Sagan, uno de los divulgadores más geniales del siglo pasado, al menos para mí... Que de pequeña me quedaba embelesada viendo COSMOS por la tele. Los subtítulos, por supuesto, son en castellano.

¿Qué es el Voyager 2? Es una sonda que se lanzó al espacio en 1977. En su viaje, se aproximó a Júpiter, Saturno, Urano y Neptuno, enviando a los científicos de la Tierra sorprendentes datos de estos planetas. Después de acercarse a Neptuno continua alejándose del Sol, nada más y nada menos que a 14,8 km/s , recorriendo 3.3 UA al año, es decir, 3.3 veces la distancia Sol-Tierra al año. A finales de 2007 se encontraba ya fuera de la influencia del Sol. Aún sigue enviando a la Tierra datos sobre los alrededores del Sistema Solar, de los cuales se desprende que el Sistema Solar no tiene forma esférica, sino ovalada.
Ni el Voyager 2, ni ninguna misión espacial hubiese sido posible sin las Matemáticas. Estas están presentes en el diseño de cada componente de la sonda, en los datos que nos envía y en la forma de interpretarlos y, por supuesto, en el cálculo de la trayectoria que se quiere que tenga. Esta se calcula meticulosamente teniendo en cuenta la influencia gravitatoria del Sol y de los planetas, lo que permite, además, un importante ahorro en el combustible. No deja de ser alucinante que la humanidad pueda diseñar y fabricar un artefacto así empujada por su curiosidad, su deseo de conocer y ayudada por su ingenio... Y después de aplicar los conocimientos matemáticos y científicos... ¡Eureka!: estamos recibiendo datos de esa maquinita que mandamos al espacio... Las Matemáticas funcionan.
Se prevé que Voyager 2 siga transmitiendo datos a la Tierra hasta el 2030... Fecha en la cual, a pesar de estar fuera del Sistema Solar, no estará aún bajo la influencia de otra estrella.
He encontrado el vídeo en forma de cómic. Aunque es en inglés, está muy bien.

Funciones. Características

Después de haber hecho la presentación con OpenOffice, se me ocurrió qué quizá sería mejor con Prezi y me quebré un poco la cabeza. Haciendo la presentación me di cuenta de que hay innumerables gráficas, pero no es tan fácil encontrarlas con magnitudes que sean familiares a los alumn@s.
Recomiendo que para verlo cliqueis en  el play, después en "MORE" y finalmente en "FULLSCREEN" para verla en pantalla completa. Cuando finaliceis solo teneis que dar a la tecla "Esc".

Funciones. Características on Prezi

Como actividad de clase, vamos a conectarnos a la página de la Red Eléctrica Española. Dentro de ella vamos a pinchar en el enlace que aparece en la columna de la derecha: "Demandas de energía eléctrica en tiempo real"

Red Eléctrica de España
En este enlace podemos ver una gráfica donde se representa el consumo de potencia eléctrica cada diez minutos.

1. ¿A qué hora se produce el mayor consumo de energía eléctrica? ¿Cuál es el valor del consumo máximo? ¿A qué crees que es debido?
2. ¿Cuándo se produce el mínimo del consumo? ¿Cuál es el valor del consumo mínimo? ¿A qué crees que es debido?
3. ¿Cuál es el consumo a las 18 h?
4. ¿Cuándo se produce un consumo de 32000 MW?
5. ¿Entre qué horas el consumo disminuye con el tiempo? ¿A qué crees que es debido?
6. ¿Entre qué horas aumenta el consumo eléctrico? ¿A qué crees que es debido?
7. ¿Qué ocurre desde las 15 h y las 18 h aproximadamente?

En la misma página aparece también las distintas fuentes que producen electricidad. Según la Red Eléctrica de España, ¿de dónde se obtiene principalmente la energía eléctrica que se produce en España?
También aparece la cantidad de CO2 asociada a la generación de energía eléctrica. ¿Dónde alcanza los extremos relativos dicha gráfica?

El hoax y los números arábigos

Últimamente he aprendido una palabra nueva: hoax. Según la Wikipedia, es una noticia falsa que comienza a circular, pretendiendo que la gente la crea verdadera. Supongo que hay una palabra en castellano para expresar eso: bulo y no sé por qué se utiliza hoax. Puede que sea por eso de que si se dice en inglés suena más interesante.

¿Cómo me enteré de este nuevo término? A propósito de los números arábigos. Si se busca un poco por ahí, es fácil encontrar la siguiente "explicación lógica" para el porqué utilizamos los símbolos que utilizamos para los números.

La verdad es que está bonita hasta llegar al 9 porque cada símbolo contiene lo que se quiere expresar. Incluso el 0: no tiene ningún ángulo. Pero la cuestión es que, en realidad, si se sigue buscando un poco más, se encuentra también que esta no es la verdadera historia de los números, sino un hoax.

Los símbolos que utilizamos para los números en todo el mundo son llamados "números arábigos" porque fueron introducidos por los árabes en Europa, aunque no fueron creados por ellos, sino que fueron inventados en la India sobre el siglo VII. Por otro lado, también existe la posibilidad de que los creadores hindúes se inspiraran en el sistema numérico que existía en aquella época en China.

En este contexto, conviene hacer una aclaración: no sólo nos referimos a los símbolos para los números del 0 al 9, sino a la forma de utilizar a estos para expresar al resto. Es decir, a nuestro sistema numérico, llamado sistema decimal o de posición. Por ejemplo, la manera de expresar trescientos cuarenta: 340 (3 centenas, 4 decenas y 0 unidades). 

Respecto a los símbolos, estos no son como los que utilizaron los hindúes en el siglo VII, ni como los que utilizaron posteriormente los árabes, como se puede ver en esta figura (si pinchas en la figura, la verás aumentada):

Nuestros símbolos provienen de los árabes occidentales. Como puede verse en el caso del 5 ha habido una gran evolución con el paso del tiempo... y no parece que los ángulos hayan jugado algún papel. También hay que decir que no guardan parecido con los símbolos hindúes, sino que los árabes ya modificaron los símbolos.

Pero lo más interesante de todo, lo realmente revolucionario, no son los símbolos para los números del 0 al 9, sino, como he dicho antes, nuestro sistema decimal o de posición, junto con la "simple" aparición del 0.

Sobre el siglo IX, el persa Al-Jwarizmi, escribió "Acerca de los cálculos con los números de la India"  Por aquel entonces, los musulmanes utilizaban el sistema numérico babilónico y ya conocían el número 0, aunque no lo utilizaban de la misma manera que los hindúes. Al-Jwarizmi fue importante en la introducción del interesante y útil sistema numérico hindú en el mundo musulmán y desde aquí al resto del mundo. Una curiosidad es que, por lo visto, en el mundo musulmán, sólo los matemáticos han utilizado el sistema decimal hasta hace poco. Tanto científicos como comerciales usaban otro sistema numérico.

Mientras tanto, en Europa se utilizaban los números romanos, los cuales no permitían hacer con facilidad operaciones con números grandes y... No usábamos el número 0. Por asombroso que nos pueda parecer, los europeos no teníamos ningún número ni símbolo en matemáticas para expresar "la nada" en la Edad Media. A finales del siglo XII, Leonardo de Pisa, también llamado Fibonacci, conoció en el Norte de África el sistema de numérico decimal a través de los árabes. Fibonacci decidió estudiarlo y aplicarlo a la contabilidad comercial, cambios de moneda y otras innumerables aplicaciones, convirtiéndose en uno de los matemáticos más destacados de la historia (por más razones). Aún así, al parecer, la introducción del sistema decimal en Europa no tuvo unos comienzos fáciles, ya que los comerciantes y la gente en general se mostraba muy desconfiada ante los nuevos métodos de cálculo. Esto último creo que queda muy bien explicado en el video "La historia del número 1". Incluso la Iglesia trató de impedir su utilización argumentando que si hacían los cálculos más sencillos y eficaces era porque eran mágicos y demoníacos. Así, los primeros calculistas que utilizaron los números y el sistema numérico actual en Europa, lo hicieron en secreto, por miedo a represalias.

No fue hasta la invención de la imprenta que "los nuevos números" se difundieron por toda Europa. En el siglo XV ya eran utilizados ampliamente.

Un par más...

Calculadora primitiva

Tema: Funciones. Caracteristicas. (4º A ESO)

Tal y como dije en clase que iba a hacer, aquí está la presentación del tema 8 del libro. Me hubiese gustado poner más ejemplos reales, pero por una cuestión de tiempo no he podido hacerlo. Otro inconveniente, aunque no sea muy importante, es que no se pueden ver las animaciones.
Recomiendo que en el menú de arriba cliqueis para verlo en modo diapositiva y en pantalla completa.  En este menú también teneis la opción de descargar.

Las simetrías del universo

Aunque la entrevista me pareció bastante interesante y entretenida, simplemente por el formato, creo que es algo árida para enseñarla en clase. Es verdad lo que el entrevistado dijo en un momento: se necesitan más "embajadores" de las Matemáticas y las Ciencias en general, que se encarguen de mostrarlas de forma amena y amable. Las Matemáticas no consisten sólo en contar y hacer operaciones aritméticas, son bastante más y, por desgracia, por alguna o varias razones, me parece muy difícil mostrar ese "bastante más" en las aulas. Aparte de esto me quedo con algunos comentarios de la entrevista como los referidos a los números primos con la esperanza de que llame la atención de algún alumn@. Es curioso que, a pesar del grado de sofisticación que se han alcanzado en las Matemáticas, aún queden problemas referidos a temas que aún se imparten en el primer curso de ESO.

MATEMATICAS EN FOTOGRAFIA

Ocurre a menudo que uno encuentra de todo menos lo que va buscando... Yo buscaba algo sobre funciones matemáticas, pero he encontrado este vídeo. Y como creo que también está bien para inspirar a los que aún no tengan ni idea de qué fotografía hacer y expresa bien la idea del concurso, aquí va. Ah... Si entrais en "youtube" podeis ver, además de este otras muchas muestras.

Como he comentado alguna vez, el truco puede estar, más que en ir buscando una fotografía "matemática" impresionante, en fijarse más en lo que nos rodea y hacer una bonita foto.

Así aprendimos a contar (Redes)

Puede que sea caer en la redundancia, pero no he podido resistirme a colgar este vídeo en el blog. Al principio de la primera entrevista comentan una tabla de arcilla del año 1500 a.C, lo cual debería, al menos, sonar a algún alumno que hubiese leído antes "¿Quién inventó las ecuaciones?" Aunque sea otra vez un vídeo (29 min) que trata del porqué empezamos a necesitar las matemáticas, es distinto de "La historia del 1" y aquí lo dejo para quien lo quiera ver, sea alumn@ o no. Cualquier comentario será bienvenido fuera o dentro del blog.

(Por cierto, Punset no es el mismo sin su característica "melena")

Redes para la Ciencia

Redes para la Ciencia

La publicidad engañosa y las Matemáticas

Si uno ve la siguiente presentación puede pensar dos cosas: uno no sabe algo tan básico como el concepto de porcentaje o las compañías de detergentes no saben matemáticas... No nos despistemos, lo segundo no ocurre. Más bien puede ocurrir lo primero o, aunque sepamos matemáticas básicas, no nos paramos unos segundos a procesar la información que nos llega.  En fin, juzgad vosotros mismos.
Inevitablemente surge también una pregunta: ¿podremos encontrar más casos como estos?

Publicidad engañosa

View more presentations from angelesrute

Historia del número 1 (The story of 1)

Tratando de historia de las Matemáticas, aquí dejo un video muy interesante, lleno de anécdotas matemáticas y de matemáticos y contado de forma muy amena.
Buen provecho.


Después de ver el video, contestar las siguientes preguntas, según lo que aparece en el video:

1. ¿De qué época es el hueso de Ishango? ¿Por qué es una prueba de que en esa época el hombre sabía contar?
2. Según el video, ¿por qué las Matemáticas se empezaron a desarrollar en Sumeria? ¿Por qué no ocurrió lo mismo en cierta tribu del centro de Australia?
3. Según el video, ¿cómo surgió la escritura en Sumeria?
4. ¿Para qué usaban los egipcios las matemáticas?
5. ¿Qué matemáticos griegos se comentan en el video?
6. ¿De dónde proviene la palabra "diezmar"?
7. ¿Por qué dejaron de utilizarse los números romanos?
8. ¿De dónde provienen los números arábigos?
9. ¿Utilizaban los romanos números muy grandes? ¿Y los hindúes? 
10. ¿Por qué tuvieron los números arábigos unos comienzos difíciles en Europa?
11. ¿De dónde proviene la palabra "bancarrota"?
12. ¿Quienes utilizaron los números arábigos por primera vez en Europa?
13. A la hora de hacer operaciones, ¿qué ventaja tiene hacerlas con números arábigos en lugar de con un ábaco?
14. Después de los números arábigos, ¿qué nuevo sistema se inventó para escribir los números? ¿Por qué es tan importante hoy en día?